Gelly: Flink Graph API
Gelly is a Graph API for Flink. It contains a set of methods and utilities which aim to simplify the development of graph analysis applications in Flink. In Gelly, graphs can be transformed and modified using high-level functions similar to the ones provided by the batch processing API. Gelly provides methods to create, transform and modify graphs, as well as a library of graph algorithms.
- Using Gelly
- Graph Representation
- Graph Creation
- Graph Properties
- Graph Transformations
- Graph Mutations
- Neighborhood Methods
- Iterative Graph Processing
- Graph Validation
- Library Methods
- Community Detection
- Label Propagation
- Connected Components
- GSA Connected Components
- PageRank
- GSA PageRank
- Single Source Shortest Paths
- GSA Single Source Shortest Paths
- Triangle Count
- Triangle Listing
- Triangle Enumerator
- Hyperlink-Induced Topic Search
- Summarization
- Adamic-Adar
- Jaccard Index
- Local Clustering Coefficient
- Global Clustering Coefficient
- Graph Algorithms
- Graph Generators
Using Gelly
Gelly is currently part of the libraries Maven project. All relevant classes are located in the org.apache.flink.graph package.
Add the following dependency to your pom.xml to use Gelly.
<dependency>
<groupId>org.apache.flink</groupId>
<artifactId>flink-gelly_2.10</artifactId>
<version>1.1.5</version>
</dependency><dependency>
<groupId>org.apache.flink</groupId>
<artifactId>flink-gelly-scala_2.10</artifactId>
<version>1.1.5</version>
</dependency>Note that Gelly is currently not part of the binary distribution. See linking with it for cluster execution here.
The remaining sections provide a description of available methods and present several examples of how to use Gelly and how to mix it with the Flink DataSet API. After reading this guide, you might also want to check the Gelly examples.
Graph Representation
In Gelly, a Graph is represented by a DataSet of vertices and a DataSet of edges.
The Graph nodes are represented by the Vertex type. A Vertex is defined by a unique ID and a value. Vertex IDs should implement the Comparable interface. Vertices without value can be represented by setting the value type to NullValue.
// create a new vertex with a Long ID and a String value
Vertex<Long, String> v = new Vertex<Long, String>(1L, "foo");
// create a new vertex with a Long ID and no value
Vertex<Long, NullValue> v = new Vertex<Long, NullValue>(1L, NullValue.getInstance());// create a new vertex with a Long ID and a String value
val v = new Vertex(1L, "foo")
// create a new vertex with a Long ID and no value
val v = new Vertex(1L, NullValue.getInstance())The graph edges are represented by the Edge type. An Edge is defined by a source ID (the ID of the source Vertex), a target ID (the ID of the target Vertex) and an optional value. The source and target IDs should be of the same type as the Vertex IDs. Edges with no value have a NullValue value type.
Edge<Long, Double> e = new Edge<Long, Double>(1L, 2L, 0.5);
// reverse the source and target of this edge
Edge<Long, Double> reversed = e.reverse();
Double weight = e.getValue(); // weight = 0.5val e = new Edge(1L, 2L, 0.5)
// reverse the source and target of this edge
val reversed = e.reverse
val weight = e.getValue // weight = 0.5In Gelly an Edge is always directed from the source vertex to the target vertex. A Graph may be undirected if for
every Edge it contains a matching Edge from the target vertex to the source vertex.
Graph Creation
You can create a Graph in the following ways:
- from a
DataSetof edges and an optionalDataSetof vertices:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Vertex<String, Long>> vertices = ...
DataSet<Edge<String, Double>> edges = ...
Graph<String, Long, Double> graph = Graph.fromDataSet(vertices, edges, env);val env = ExecutionEnvironment.getExecutionEnvironment
val vertices: DataSet[Vertex[String, Long]] = ...
val edges: DataSet[Edge[String, Double]] = ...
val graph = Graph.fromDataSet(vertices, edges, env)- from a
DataSetofTuple2representing the edges. Gelly will convert eachTuple2to anEdge, where the first field will be the source ID and the second field will be the target ID. Both vertex and edge values will be set toNullValue.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Tuple2<String, String>> edges = ...
Graph<String, NullValue, NullValue> graph = Graph.fromTuple2DataSet(edges, env);val env = ExecutionEnvironment.getExecutionEnvironment
val edges: DataSet[(String, String)] = ...
val graph = Graph.fromTuple2DataSet(edges, env)- from a
DataSetofTuple3and an optionalDataSetofTuple2. In this case, Gelly will convert eachTuple3to anEdge, where the first field will be the source ID, the second field will be the target ID and the third field will be the edge value. Equivalently, eachTuple2will be converted to aVertex, where the first field will be the vertex ID and the second field will be the vertex value:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
DataSet<Tuple2<String, Long>> vertexTuples = env.readCsvFile("path/to/vertex/input").types(String.class, Long.class);
DataSet<Tuple3<String, String, Double>> edgeTuples = env.readCsvFile("path/to/edge/input").types(String.class, String.class, Double.class);
Graph<String, Long, Double> graph = Graph.fromTupleDataSet(vertexTuples, edgeTuples, env);-
from a CSV file of Edge data and an optional CSV file of Vertex data. In this case, Gelly will convert each row from the Edge CSV file to an
Edge, where the first field will be the source ID, the second field will be the target ID and the third field (if present) will be the edge value. Equivalently, each row from the optional Vertex CSV file will be converted to aVertex, where the first field will be the vertex ID and the second field (if present) will be the vertex value. In order to get aGraphfrom aGraphCsvReaderone has to specify the types, using one of the following methods: types(Class<K> vertexKey, Class<VV> vertexValue,Class<EV> edgeValue): both vertex and edge values are present.edgeTypes(Class<K> vertexKey, Class<EV> edgeValue): the Graph has edge values, but no vertex values.vertexTypes(Class<K> vertexKey, Class<VV> vertexValue): the Graph has vertex values, but no edge values.keyType(Class<K> vertexKey): the Graph has no vertex values and no edge values.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create a Graph with String Vertex IDs, Long Vertex values and Double Edge values
Graph<String, Long, Double> graph = Graph.fromCsvReader("path/to/vertex/input", "path/to/edge/input", env)
.types(String.class, Long.class, Double.class);
// create a Graph with neither Vertex nor Edge values
Graph<Long, NullValue, NullValue> simpleGraph = Graph.fromCsvReader("path/to/edge/input", env).keyType(Long.class);val env = ExecutionEnvironment.getExecutionEnvironment
val vertexTuples = env.readCsvFile[String, Long]("path/to/vertex/input")
val edgeTuples = env.readCsvFile[String, String, Double]("path/to/edge/input")
val graph = Graph.fromTupleDataSet(vertexTuples, edgeTuples, env)- from a CSV file of Edge data and an optional CSV file of Vertex data.
In this case, Gelly will convert each row from the Edge CSV file to an
Edge. The first field of the each row will be the source ID, the second field will be the target ID and the third field (if present) will be the edge value. If the edges have no associated value, set the edge value type parameter (3rd type argument) toNullValue. You can also specify that the vertices are initialized with a vertex value. If you provide a path to a CSV file viapathVertices, each row of this file will be converted to aVertex. The first field of each row will be the vertex ID and the second field will be the vertex value. If you provide a vertex value initializerMapFunctionvia thevertexValueInitializerparameter, then this function is used to generate the vertex values. The set of vertices will be created automatically from the edges input. If the vertices have no associated value, set the vertex value type parameter (2nd type argument) toNullValue. The vertices will then be automatically created from the edges input with vertex value of typeNullValue.
val env = ExecutionEnvironment.getExecutionEnvironment
// create a Graph with String Vertex IDs, Long Vertex values and Double Edge values
val graph = Graph.fromCsvReader[String, Long, Double](
pathVertices = "path/to/vertex/input",
pathEdges = "path/to/edge/input",
env = env)
// create a Graph with neither Vertex nor Edge values
val simpleGraph = Graph.fromCsvReader[Long, NullValue, NullValue](
pathEdges = "path/to/edge/input",
env = env)
// create a Graph with Double Vertex values generated by a vertex value initializer and no Edge values
val simpleGraph = Graph.fromCsvReader[Long, Double, NullValue](
pathEdges = "path/to/edge/input",
vertexValueInitializer = new MapFunction[Long, Double]() {
def map(id: Long): Double = {
id.toDouble
}
},
env = env)- from a
Collectionof edges and an optionalCollectionof vertices:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
List<Vertex<Long, Long>> vertexList = new ArrayList...
List<Edge<Long, String>> edgeList = new ArrayList...
Graph<Long, Long, String> graph = Graph.fromCollection(vertexList, edgeList, env);If no vertex input is provided during Graph creation, Gelly will automatically produce the Vertex DataSet from the edge input. In this case, the created vertices will have no values. Alternatively, you can provide a MapFunction as an argument to the creation method, in order to initialize the Vertex values:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// initialize the vertex value to be equal to the vertex ID
Graph<Long, Long, String> graph = Graph.fromCollection(edgeList,
new MapFunction<Long, Long>() {
public Long map(Long value) {
return value;
}
}, env);val env = ExecutionEnvironment.getExecutionEnvironment
val vertexList = List(...)
val edgeList = List(...)
val graph = Graph.fromCollection(vertexList, edgeList, env)If no vertex input is provided during Graph creation, Gelly will automatically produce the Vertex DataSet from the edge input. In this case, the created vertices will have no values. Alternatively, you can provide a MapFunction as an argument to the creation method, in order to initialize the Vertex values:
val env = ExecutionEnvironment.getExecutionEnvironment
// initialize the vertex value to be equal to the vertex ID
val graph = Graph.fromCollection(edgeList,
new MapFunction[Long, Long] {
def map(id: Long): Long = id
}, env)Graph Properties
Gelly includes the following methods for retrieving various Graph properties and metrics:
// get the Vertex DataSet
DataSet<Vertex<K, VV>> getVertices()
// get the Edge DataSet
DataSet<Edge<K, EV>> getEdges()
// get the IDs of the vertices as a DataSet
DataSet<K> getVertexIds()
// get the source-target pairs of the edge IDs as a DataSet
DataSet<Tuple2<K, K>> getEdgeIds()
// get a DataSet of <vertex ID, in-degree> pairs for all vertices
DataSet<Tuple2<K, LongValue>> inDegrees()
// get a DataSet of <vertex ID, out-degree> pairs for all vertices
DataSet<Tuple2<K, LongValue>> outDegrees()
// get a DataSet of <vertex ID, degree> pairs for all vertices, where degree is the sum of in- and out- degrees
DataSet<Tuple2<K, LongValue>> getDegrees()
// get the number of vertices
long numberOfVertices()
// get the number of edges
long numberOfEdges()
// get a DataSet of Triplets<srcVertex, trgVertex, edge>
DataSet<Triplet<K, VV, EV>> getTriplets()// get the Vertex DataSet
getVertices: DataSet[Vertex[K, VV]]
// get the Edge DataSet
getEdges: DataSet[Edge[K, EV]]
// get the IDs of the vertices as a DataSet
getVertexIds: DataSet[K]
// get the source-target pairs of the edge IDs as a DataSet
getEdgeIds: DataSet[(K, K)]
// get a DataSet of <vertex ID, in-degree> pairs for all vertices
inDegrees: DataSet[(K, LongValue)]
// get a DataSet of <vertex ID, out-degree> pairs for all vertices
outDegrees: DataSet[(K, LongValue)]
// get a DataSet of <vertex ID, degree> pairs for all vertices, where degree is the sum of in- and out- degrees
getDegrees: DataSet[(K, LongValue)]
// get the number of vertices
numberOfVertices: Long
// get the number of edges
numberOfEdges: Long
// get a DataSet of Triplets<srcVertex, trgVertex, edge>
getTriplets: DataSet[Triplet[K, VV, EV]]Graph Transformations
- Map: Gelly provides specialized methods for applying a map transformation on the vertex values or edge values.
mapVerticesandmapEdgesreturn a newGraph, where the IDs of the vertices (or edges) remain unchanged, while the values are transformed according to the provided user-defined map function. The map functions also allow changing the type of the vertex or edge values.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
Graph<Long, Long, Long> graph = Graph.fromDataSet(vertices, edges, env);
// increment each vertex value by one
Graph<Long, Long, Long> updatedGraph = graph.mapVertices(
new MapFunction<Vertex<Long, Long>, Long>() {
public Long map(Vertex<Long, Long> value) {
return value.getValue() + 1;
}
});val env = ExecutionEnvironment.getExecutionEnvironment
val graph = Graph.fromDataSet(vertices, edges, env)
// increment each vertex value by one
val updatedGraph = graph.mapVertices(v => v.getValue + 1)- Translate: Gelly provides specialized methods for translating the value and/or type of vertex and edge IDs (
translateGraphIDs), vertex values (translateVertexValues), or edge values (translateEdgeValues). Translation is performed by the user-defined map function, several of which are provided in theorg.apache.flink.graph.asm.translatepackage. The sameMapFunctioncan be used for all the three translate methods.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
Graph<Long, Long, Long> graph = Graph.fromDataSet(vertices, edges, env);
// translate each vertex and edge ID to a String
Graph<String, Long, Long> updatedGraph = graph.translateGraphIds(
new MapFunction<Long, String>() {
public String map(Long id) {
return id.toString();
}
});
// translate vertex IDs, edge IDs, vertex values, and edge values to LongValue
Graph<LongValue, LongValue, LongValue> updatedGraph = graph
.translateGraphIds(new LongToLongValue())
.translateVertexValues(new LongToLongValue())
.translateEdgeValues(new LongToLongValue())val env = ExecutionEnvironment.getExecutionEnvironment
val graph = Graph.fromDataSet(vertices, edges, env)
// translate each vertex and edge ID to a String
val updatedGraph = graph.translateGraphIds(id => id.toString)- Filter: A filter transformation applies a user-defined filter function on the vertices or edges of the
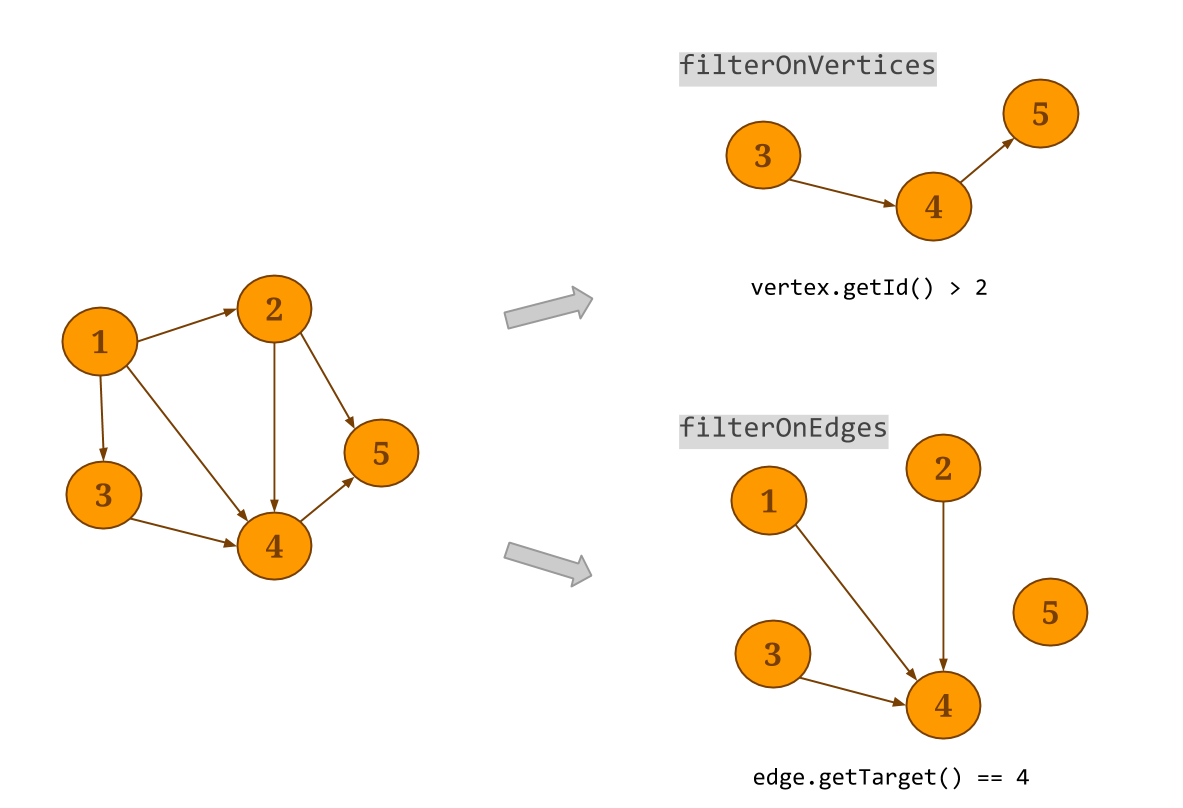
Graph.filterOnEdgeswill create a sub-graph of the original graph, keeping only the edges that satisfy the provided predicate. Note that the vertex dataset will not be modified. Respectively,filterOnVerticesapplies a filter on the vertices of the graph. Edges whose source and/or target do not satisfy the vertex predicate are removed from the resulting edge dataset. Thesubgraphmethod can be used to apply a filter function to the vertices and the edges at the same time.
Graph<Long, Long, Long> graph = ...
graph.subgraph(
new FilterFunction<Vertex<Long, Long>>() {
public boolean filter(Vertex<Long, Long> vertex) {
// keep only vertices with positive values
return (vertex.getValue() > 0);
}
},
new FilterFunction<Edge<Long, Long>>() {
public boolean filter(Edge<Long, Long> edge) {
// keep only edges with negative values
return (edge.getValue() < 0);
}
})val graph: Graph[Long, Long, Long] = ...
// keep only vertices with positive values
// and only edges with negative values
graph.subgraph((vertex => vertex.getValue > 0), (edge => edge.getValue < 0))
- Join: Gelly provides specialized methods for joining the vertex and edge datasets with other input datasets.
joinWithVerticesjoins the vertices with aTuple2input data set. The join is performed using the vertex ID and the first field of theTuple2input as the join keys. The method returns a newGraphwhere the vertex values have been updated according to a provided user-defined transformation function. Similarly, an input dataset can be joined with the edges, using one of three methods.joinWithEdgesexpects an inputDataSetofTuple3and joins on the composite key of both source and target vertex IDs.joinWithEdgesOnSourceexpects aDataSetofTuple2and joins on the source key of the edges and the first attribute of the input dataset andjoinWithEdgesOnTargetexpects aDataSetofTuple2and joins on the target key of the edges and the first attribute of the input dataset. All three methods apply a transformation function on the edge and the input data set values. Note that if the input dataset contains a key multiple times, all Gelly join methods will only consider the first value encountered.
Graph<Long, Double, Double> network = ...
DataSet<Tuple2<Long, LongValue>> vertexOutDegrees = network.outDegrees();
// assign the transition probabilities as the edge weights
Graph<Long, Double, Double> networkWithWeights = network.joinWithEdgesOnSource(vertexOutDegrees,
new VertexJoinFunction<Double, LongValue>() {
public Double vertexJoin(Double vertexValue, LongValue inputValue) {
return vertexValue / inputValue.getValue();
}
});val network: Graph[Long, Double, Double] = ...
val vertexOutDegrees: DataSet[(Long, LongValue)] = network.outDegrees
// assign the transition probabilities as the edge weights
val networkWithWeights = network.joinWithEdgesOnSource(vertexOutDegrees, (v1: Double, v2: LongValue) => v1 / v2.getValue)-
Reverse: the
reverse()method returns a newGraphwhere the direction of all edges has been reversed. -
Undirected: In Gelly, a
Graphis always directed. Undirected graphs can be represented by adding all opposite-direction edges to a graph. For this purpose, Gelly provides thegetUndirected()method. -
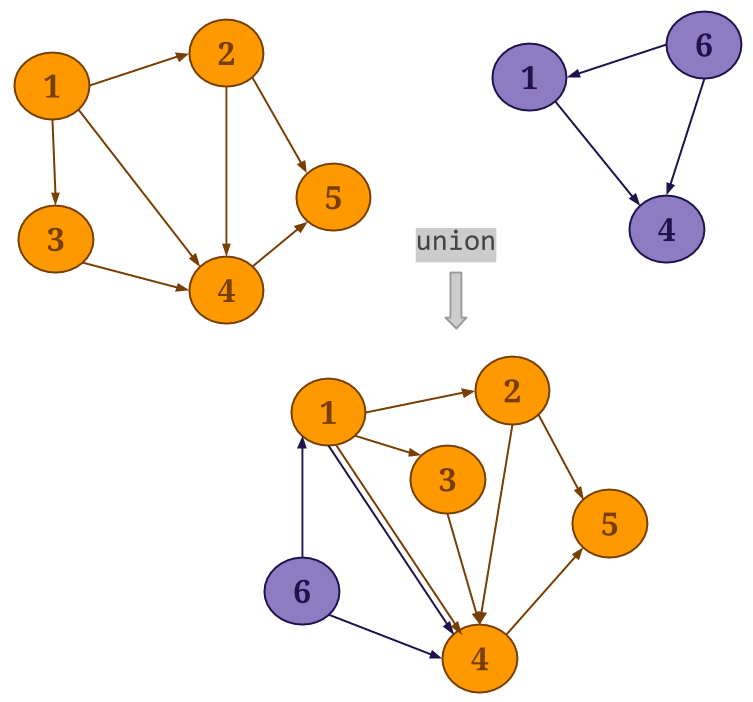
Union: Gelly’s
union()method performs a union operation on the vertex and edge sets of the specified graph and the current graph. Duplicate vertices are removed from the resultingGraph, while if duplicate edges exist, these will be preserved.
-
Difference: Gelly’s
difference()method performs a difference on the vertex and edge sets of the current graph and the specified graph. -
Intersect: Gelly’s
intersect()method performs an intersect on the edge sets of the current graph and the specified graph. The result is a newGraphthat contains all edges that exist in both input graphs. Two edges are considered equal, if they have the same source identifier, target identifier and edge value. Vertices in the resulting graph have no value. If vertex values are required, one can for example retrieve them from one of the input graphs using thejoinWithVertices()method. Depending on the parameterdistinct, equal edges are either contained once in the resultingGraphor as often as there are pairs of equal edges in the input graphs.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create first graph from edges {(1, 3, 12) (1, 3, 13), (1, 3, 13)}
List<Edge<Long, Long>> edges1 = ...
Graph<Long, NullValue, Long> graph1 = Graph.fromCollection(edges1, env);
// create second graph from edges {(1, 3, 13)}
List<Edge<Long, Long>> edges2 = ...
Graph<Long, NullValue, Long> graph2 = Graph.fromCollection(edges2, env);
// Using distinct = true results in {(1,3,13)}
Graph<Long, NullValue, Long> intersect1 = graph1.intersect(graph2, true);
// Using distinct = false results in {(1,3,13),(1,3,13)} as there is one edge pair
Graph<Long, NullValue, Long> intersect2 = graph1.intersect(graph2, false);val env = ExecutionEnvironment.getExecutionEnvironment
// create first graph from edges {(1, 3, 12) (1, 3, 13), (1, 3, 13)}
val edges1: List[Edge[Long, Long]] = ...
val graph1 = Graph.fromCollection(edges1, env)
// create second graph from edges {(1, 3, 13)}
val edges2: List[Edge[Long, Long]] = ...
val graph2 = Graph.fromCollection(edges2, env)
// Using distinct = true results in {(1,3,13)}
val intersect1 = graph1.intersect(graph2, true)
// Using distinct = false results in {(1,3,13),(1,3,13)} as there is one edge pair
val intersect2 = graph1.intersect(graph2, false)Graph Mutations
Gelly includes the following methods for adding and removing vertices and edges from an input Graph:
// adds a Vertex to the Graph. If the Vertex already exists, it will not be added again.
Graph<K, VV, EV> addVertex(final Vertex<K, VV> vertex)
// adds a list of vertices to the Graph. If the vertices already exist in the graph, they will not be added once more.
Graph<K, VV, EV> addVertices(List<Vertex<K, VV>> verticesToAdd)
// adds an Edge to the Graph. If the source and target vertices do not exist in the graph, they will also be added.
Graph<K, VV, EV> addEdge(Vertex<K, VV> source, Vertex<K, VV> target, EV edgeValue)
// adds a list of edges to the Graph. When adding an edge for a non-existing set of vertices, the edge is considered invalid and ignored.
Graph<K, VV, EV> addEdges(List<Edge<K, EV>> newEdges)
// removes the given Vertex and its edges from the Graph.
Graph<K, VV, EV> removeVertex(Vertex<K, VV> vertex)
// removes the given list of vertices and their edges from the Graph
Graph<K, VV, EV> removeVertices(List<Vertex<K, VV>> verticesToBeRemoved)
// removes *all* edges that match the given Edge from the Graph.
Graph<K, VV, EV> removeEdge(Edge<K, EV> edge)
// removes *all* edges that match the edges in the given list
Graph<K, VV, EV> removeEdges(List<Edge<K, EV>> edgesToBeRemoved)// adds a Vertex to the Graph. If the Vertex already exists, it will not be added again.
addVertex(vertex: Vertex[K, VV])
// adds a list of vertices to the Graph. If the vertices already exist in the graph, they will not be added once more.
addVertices(verticesToAdd: List[Vertex[K, VV]])
// adds an Edge to the Graph. If the source and target vertices do not exist in the graph, they will also be added.
addEdge(source: Vertex[K, VV], target: Vertex[K, VV], edgeValue: EV)
// adds a list of edges to the Graph. When adding an edge for a non-existing set of vertices, the edge is considered invalid and ignored.
addEdges(edges: List[Edge[K, EV]])
// removes the given Vertex and its edges from the Graph.
removeVertex(vertex: Vertex[K, VV])
// removes the given list of vertices and their edges from the Graph
removeVertices(verticesToBeRemoved: List[Vertex[K, VV]])
// removes *all* edges that match the given Edge from the Graph.
removeEdge(edge: Edge[K, EV])
// removes *all* edges that match the edges in the given list
removeEdges(edgesToBeRemoved: List[Edge[K, EV]])Neighborhood Methods
Neighborhood methods allow vertices to perform an aggregation on their first-hop neighborhood.
reduceOnEdges() can be used to compute an aggregation on the values of the neighboring edges of a vertex and reduceOnNeighbors() can be used to compute an aggregation on the values of the neighboring vertices. These methods assume associative and commutative aggregations and exploit combiners internally, significantly improving performance.
The neighborhood scope is defined by the EdgeDirection parameter, which takes the values IN, OUT or ALL. IN will gather all in-coming edges (neighbors) of a vertex, OUT will gather all out-going edges (neighbors), while ALL will gather all edges (neighbors).
For example, assume that you want to select the minimum weight of all out-edges for each vertex in the following graph:
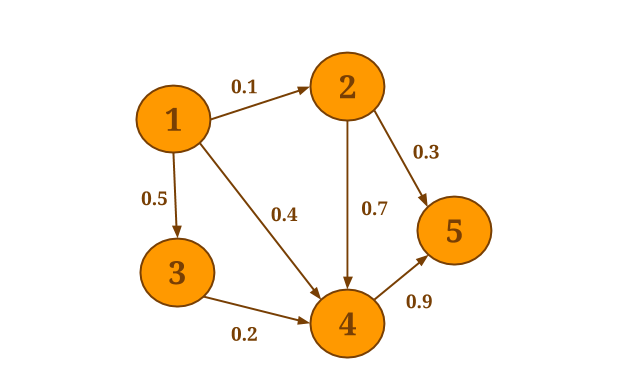
The following code will collect the out-edges for each vertex and apply the SelectMinWeight() user-defined function on each of the resulting neighborhoods:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Long, Double>> minWeights = graph.reduceOnEdges(new SelectMinWeight(), EdgeDirection.OUT);
// user-defined function to select the minimum weight
static final class SelectMinWeight implements ReduceEdgesFunction<Double> {
@Override
public Double reduceEdges(Double firstEdgeValue, Double secondEdgeValue) {
return Math.min(firstEdgeValue, secondEdgeValue);
}
}val graph: Graph[Long, Long, Double] = ...
val minWeights = graph.reduceOnEdges(new SelectMinWeight, EdgeDirection.OUT)
// user-defined function to select the minimum weight
final class SelectMinWeight extends ReduceEdgesFunction[Double] {
override def reduceEdges(firstEdgeValue: Double, secondEdgeValue: Double): Double = {
Math.min(firstEdgeValue, secondEdgeValue)
}
}
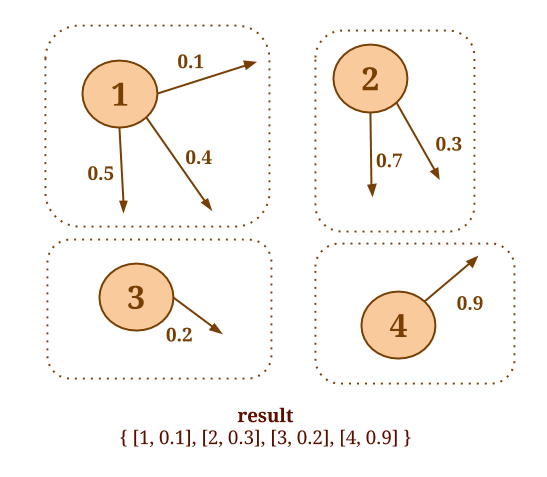
Similarly, assume that you would like to compute the sum of the values of all in-coming neighbors, for every vertex. The following code will collect the in-coming neighbors for each vertex and apply the SumValues() user-defined function on each neighborhood:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Long, Long>> verticesWithSum = graph.reduceOnNeighbors(new SumValues(), EdgeDirection.IN);
// user-defined function to sum the neighbor values
static final class SumValues implements ReduceNeighborsFunction<Long> {
@Override
public Long reduceNeighbors(Long firstNeighbor, Long secondNeighbor) {
return firstNeighbor + secondNeighbor;
}
}val graph: Graph[Long, Long, Double] = ...
val verticesWithSum = graph.reduceOnNeighbors(new SumValues, EdgeDirection.IN)
// user-defined function to sum the neighbor values
final class SumValues extends ReduceNeighborsFunction[Long] {
override def reduceNeighbors(firstNeighbor: Long, secondNeighbor: Long): Long = {
firstNeighbor + secondNeighbor
}
}
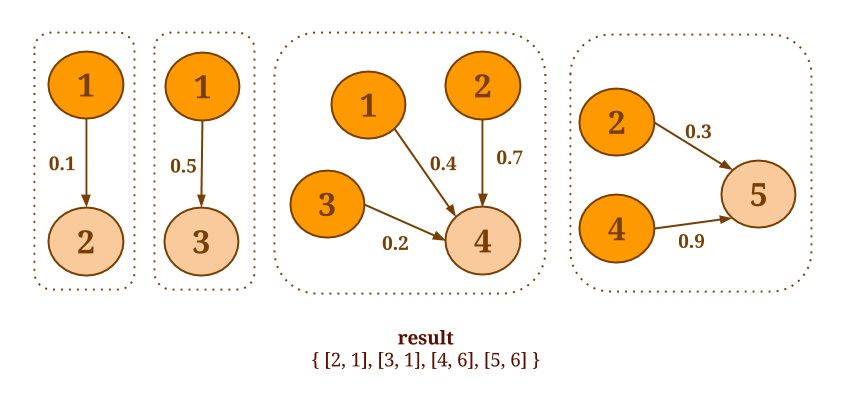
When the aggregation function is not associative and commutative or when it is desirable to return more than one values per vertex, one can use the more general
groupReduceOnEdges() and groupReduceOnNeighbors() methods.
These methods return zero, one or more values per vertex and provide access to the whole neighborhood.
For example, the following code will output all the vertex pairs which are connected with an edge having a weight of 0.5 or more:
Graph<Long, Long, Double> graph = ...
DataSet<Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> vertexPairs = graph.groupReduceOnNeighbors(new SelectLargeWeightNeighbors(), EdgeDirection.OUT);
// user-defined function to select the neighbors which have edges with weight > 0.5
static final class SelectLargeWeightNeighbors implements NeighborsFunctionWithVertexValue<Long, Long, Double,
Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> {
@Override
public void iterateNeighbors(Vertex<Long, Long> vertex,
Iterable<Tuple2<Edge<Long, Double>, Vertex<Long, Long>>> neighbors,
Collector<Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>> out) {
for (Tuple2<Edge<Long, Double>, Vertex<Long, Long>> neighbor : neighbors) {
if (neighbor.f0.f2 > 0.5) {
out.collect(new Tuple2<Vertex<Long, Long>, Vertex<Long, Long>>(vertex, neighbor.f1));
}
}
}
}val graph: Graph[Long, Long, Double] = ...
val vertexPairs = graph.groupReduceOnNeighbors(new SelectLargeWeightNeighbors, EdgeDirection.OUT)
// user-defined function to select the neighbors which have edges with weight > 0.5
final class SelectLargeWeightNeighbors extends NeighborsFunctionWithVertexValue[Long, Long, Double,
(Vertex[Long, Long], Vertex[Long, Long])] {
override def iterateNeighbors(vertex: Vertex[Long, Long],
neighbors: Iterable[(Edge[Long, Double], Vertex[Long, Long])],
out: Collector[(Vertex[Long, Long], Vertex[Long, Long])]) = {
for (neighbor <- neighbors) {
if (neighbor._1.getValue() > 0.5) {
out.collect(vertex, neighbor._2);
}
}
}
}When the aggregation computation does not require access to the vertex value (for which the aggregation is performed), it is advised to use the more efficient EdgesFunction and NeighborsFunction for the user-defined functions. When access to the vertex value is required, one should use EdgesFunctionWithVertexValue and NeighborsFunctionWithVertexValue instead.
Iterative Graph Processing
Gelly exploits Flink’s efficient iteration operators to support large-scale iterative graph processing. Currently, we provide implementations of the vertex-centric, scatter-gather, and gather-sum-apply models. In the following sections, we describe these abstractions and show how you can use them in Gelly.
Vertex-Centric Iterations
The vertex-centric model, also known as “think like a vertex” or “Pregel”, expresses computation from the perspective of a vertex in the graph. The computation proceeds in synchronized iteration steps, called supersteps. In each superstep, each vertex executes one user-defined function. Vertices communicate with other vertices through messages. A vertex can send a message to any other vertex in the graph, as long as it knows its unique ID.
The computational model is shown in the figure below. The dotted boxes correspond to parallelization units. In each superstep, all active vertices execute the same user-defined computation in parallel. Supersteps are executed synchronously, so that messages sent during one superstep are guaranteed to be delivered in the beginning of the next superstep.
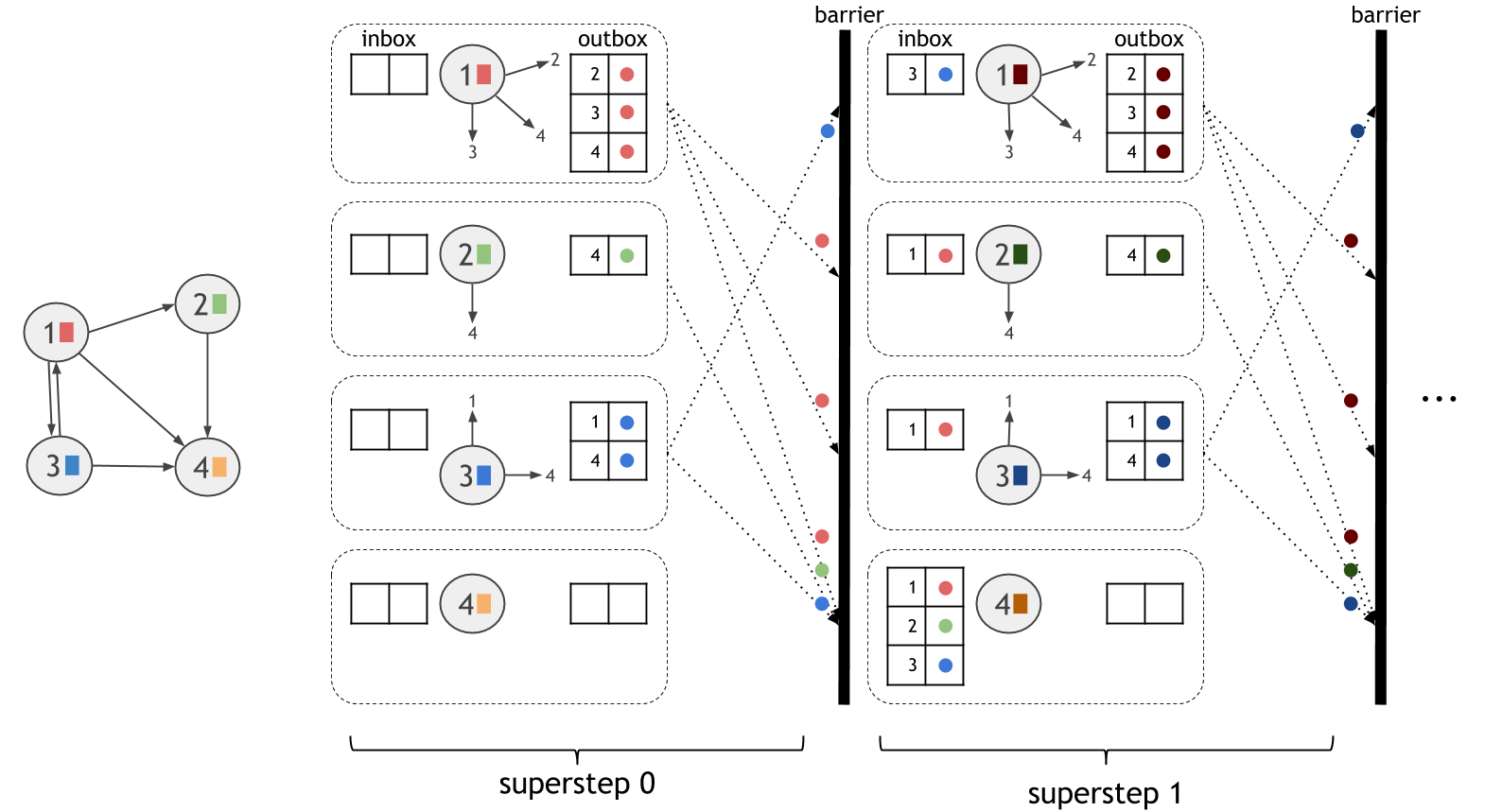
To use vertex-centric iterations in Gelly, the user only needs to define the vertex compute function, ComputeFunction.
This function and the maximum number of iterations to run are given as parameters to Gelly’s runVertexCentricIteration. This method will execute the vertex-centric iteration on the input Graph and return a new Graph, with updated vertex values. An optional message combiner, MessageCombiner, can be defined to reduce communication costs.
Let us consider computing Single-Source-Shortest-Paths with vertex-centric iterations. Initially, each vertex has a value of infinite distance, except from the source vertex, which has a value of zero. During the first superstep, the source propagates distances to its neighbors. During the following supersteps, each vertex checks its received messages and chooses the minimum distance among them. If this distance is smaller than its current value, it updates its state and produces messages for its neighbors. If a vertex does not change its value during a superstep, then it does not produce any messages for its neighbors for the next superstep. The algorithm converges when there are no value updates or the maximum number of supersteps has been reached. In this algorithm, a message combiner can be used to reduce the number of messages sent to a target vertex.
// read the input graph
Graph<Long, Double, Double> graph = ...
// define the maximum number of iterations
int maxIterations = 10;
// Execute the vertex-centric iteration
Graph<Long, Double, Double> result = graph.runVertexCentricIteration(
new SSSPComputeFunction(), new SSSPCombiner(), maxIterations);
// Extract the vertices as the result
DataSet<Vertex<Long, Double>> singleSourceShortestPaths = result.getVertices();
// - - - UDFs - - - //
public static final class SSSPComputeFunction extends ComputeFunction<Long, Double, Double, Double> {
public void compute(Vertex<Long, Double> vertex, MessageIterator<Double> messages) {
double minDistance = (vertex.getId().equals(srcId)) ? 0d : Double.POSITIVE_INFINITY;
for (Double msg : messages) {
minDistance = Math.min(minDistance, msg);
}
if (minDistance < vertex.getValue()) {
setNewVertexValue(minDistance);
for (Edge<Long, Double> e: getEdges()) {
sendMessageTo(e.getTarget(), minDistance + e.getValue());
}
}
}
// message combiner
public static final class SSSPCombiner extends MessageCombiner<Long, Double> {
public void combineMessages(MessageIterator<Double> messages) {
double minMessage = Double.POSITIVE_INFINITY;
for (Double msg: messages) {
minMessage = Math.min(minMessage, msg);
}
sendCombinedMessage(minMessage);
}
}// read the input graph
val graph: Graph[Long, Double, Double] = ...
// define the maximum number of iterations
val maxIterations = 10
// Execute the vertex-centric iteration
val result = graph.runVertexCentricIteration(new SSSPComputeFunction, new SSSPCombiner, maxIterations)
// Extract the vertices as the result
val singleSourceShortestPaths = result.getVertices
// - - - UDFs - - - //
final class SSSPComputeFunction extends ComputeFunction[Long, Double, Double, Double] {
override def compute(vertex: Vertex[Long, Double], messages: MessageIterator[Double]) = {
var minDistance = if (vertex.getId.equals(srcId)) 0 else Double.MaxValue
while (messages.hasNext) {
val msg = messages.next
if (msg < minDistance) {
minDistance = msg
}
}
if (vertex.getValue > minDistance) {
setNewVertexValue(minDistance)
for (edge: Edge[Long, Double] <- getEdges) {
sendMessageTo(edge.getTarget, vertex.getValue + edge.getValue)
}
}
}
// message combiner
final class SSSPCombiner extends MessageCombiner[Long, Double] {
override def combineMessages(messages: MessageIterator[Double]) {
var minDistance = Double.MaxValue
while (messages.hasNext) {
val msg = inMessages.next
if (msg < minDistance) {
minDistance = msg
}
}
sendCombinedMessage(minMessage)
}
}Configuring a Vertex-Centric Iteration
A vertex-centric iteration can be configured using a VertexCentricConfiguration object.
Currently, the following parameters can be specified:
-
Name: The name for the vertex-centric iteration. The name is displayed in logs and messages and can be specified using the
setName()method. -
Parallelism: The parallelism for the iteration. It can be set using the
setParallelism()method. -
Solution set in unmanaged memory: Defines whether the solution set is kept in managed memory (Flink’s internal way of keeping objects in serialized form) or as a simple object map. By default, the solution set runs in managed memory. This property can be set using the
setSolutionSetUnmanagedMemory()method. -
Aggregators: Iteration aggregators can be registered using the
registerAggregator()method. An iteration aggregator combines all aggregates globally once per superstep and makes them available in the next superstep. Registered aggregators can be accessed inside the user-definedComputeFunction. -
Broadcast Variables: DataSets can be added as Broadcast Variables to the
ComputeFunction, using theaddBroadcastSet()method.
Graph<Long, Double, Double> graph = ...
// configure the iteration
VertexCentricConfiguration parameters = new VertexCentricConfiguration();
// set the iteration name
parameters.setName("Gelly Iteration");
// set the parallelism
parameters.setParallelism(16);
// register an aggregator
parameters.registerAggregator("sumAggregator", new LongSumAggregator());
// run the vertex-centric iteration, also passing the configuration parameters
Graph<Long, Long, Double> result =
graph.runVertexCentricIteration(
new Compute(), null, maxIterations, parameters);
// user-defined function
public static final class Compute extends ComputeFunction {
LongSumAggregator aggregator = new LongSumAggregator();
public void preSuperstep() {
// retrieve the Aggregator
aggregator = getIterationAggregator("sumAggregator");
}
public void compute(Vertex<Long, Long> vertex, MessageIterator inMessages) {
//do some computation
Long partialValue = ...
// aggregate the partial value
aggregator.aggregate(partialValue);
// update the vertex value
setNewVertexValue(...);
}
}val graph: Graph[Long, Long, Double] = ...
val parameters = new VertexCentricConfiguration
// set the iteration name
parameters.setName("Gelly Iteration")
// set the parallelism
parameters.setParallelism(16)
// register an aggregator
parameters.registerAggregator("sumAggregator", new LongSumAggregator)
// run the vertex-centric iteration, also passing the configuration parameters
val result = graph.runVertexCentricIteration(new Compute, new Combiner, maxIterations, parameters)
// user-defined function
final class Compute extends ComputeFunction {
var aggregator = new LongSumAggregator
override def preSuperstep {
// retrieve the Aggregator
aggregator = getIterationAggregator("sumAggregator")
}
override def compute(vertex: Vertex[Long, Long], inMessages: MessageIterator[Long]) {
//do some computation
val partialValue = ...
// aggregate the partial value
aggregator.aggregate(partialValue)
// update the vertex value
setNewVertexValue(...)
}
}Scatter-Gather Iterations
The scatter-gather model, also known as “signal/collect” model, expresses computation from the perspective of a vertex in the graph. The computation proceeds in synchronized iteration steps, called supersteps. In each superstep, a vertex produces messages for other vertices and updates its value based on the messages it receives. To use scatter-gather iterations in Gelly, the user only needs to define how a vertex behaves in each superstep:
- Scatter: produces the messages that a vertex will send to other vertices.
- Gather: updates the vertex value using received messages.
Gelly provides methods for scatter-gather iterations. The user only needs to implement two functions, corresponding to the scatter and gather phases. The first function is a ScatterFunction, which allows a vertex to send out messages to other vertices. Messages are received during the same superstep as they are sent. The second function is GatherFunction, which defines how a vertex will update its value based on the received messages.
These functions and the maximum number of iterations to run are given as parameters to Gelly’s runScatterGatherIteration. This method will execute the scatter-gather iteration on the input Graph and return a new Graph, with updated vertex values.
A scatter-gather iteration can be extended with information such as the total number of vertices, the in degree and out degree. Additionally, the neighborhood type (in/out/all) over which to run the scatter-gather iteration can be specified. By default, the updates from the in-neighbors are used to modify the current vertex’s state and messages are sent to out-neighbors.
Let us consider computing Single-Source-Shortest-Paths with scatter-gather iterations on the following graph and let vertex 1 be the source. In each superstep, each vertex sends a candidate distance message to all its neighbors. The message value is the sum of the current value of the vertex and the edge weight connecting this vertex with its neighbor. Upon receiving candidate distance messages, each vertex calculates the minimum distance and, if a shorter path has been discovered, it updates its value. If a vertex does not change its value during a superstep, then it does not produce messages for its neighbors for the next superstep. The algorithm converges when there are no value updates.
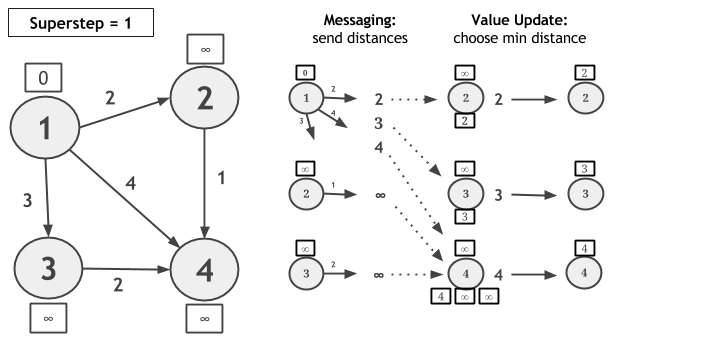
// read the input graph
Graph<Long, Double, Double> graph = ...
// define the maximum number of iterations
int maxIterations = 10;
// Execute the scatter-gather iteration
Graph<Long, Double, Double> result = graph.runScatterGatherIteration(
new MinDistanceMessenger(), new VertexDistanceUpdater(), maxIterations);
// Extract the vertices as the result
DataSet<Vertex<Long, Double>> singleSourceShortestPaths = result.getVertices();
// - - - UDFs - - - //
// scatter: messaging
public static final class MinDistanceMessenger extends ScatterFunction<Long, Double, Double, Double> {
public void sendMessages(Vertex<Long, Double> vertex) {
for (Edge<Long, Double> edge : getEdges()) {
sendMessageTo(edge.getTarget(), vertex.getValue() + edge.getValue());
}
}
}
// gather: vertex update
public static final class VertexDistanceUpdater extends GatherFunction<Long, Double, Double> {
public void updateVertex(Vertex<Long, Double> vertex, MessageIterator<Double> inMessages) {
Double minDistance = Double.MAX_VALUE;
for (double msg : inMessages) {
if (msg < minDistance) {
minDistance = msg;
}
}
if (vertex.getValue() > minDistance) {
setNewVertexValue(minDistance);
}
}
}// read the input graph
val graph: Graph[Long, Double, Double] = ...
// define the maximum number of iterations
val maxIterations = 10
// Execute the scatter-gather iteration
val result = graph.runScatterGatherIteration(new MinDistanceMessenger, new VertexDistanceUpdater, maxIterations)
// Extract the vertices as the result
val singleSourceShortestPaths = result.getVertices
// - - - UDFs - - - //
// messaging
final class MinDistanceMessenger extends ScatterFunction[Long, Double, Double, Double] {
override def sendMessages(vertex: Vertex[Long, Double]) = {
for (edge: Edge[Long, Double] <- getEdges) {
sendMessageTo(edge.getTarget, vertex.getValue + edge.getValue)
}
}
}
// vertex update
final class VertexDistanceUpdater extends GatherFunction[Long, Double, Double] {
override def updateVertex(vertex: Vertex[Long, Double], inMessages: MessageIterator[Double]) = {
var minDistance = Double.MaxValue
while (inMessages.hasNext) {
val msg = inMessages.next
if (msg < minDistance) {
minDistance = msg
}
}
if (vertex.getValue > minDistance) {
setNewVertexValue(minDistance)
}
}
}Configuring a Scatter-Gather Iteration
A scatter-gather iteration can be configured using a ScatterGatherConfiguration object.
Currently, the following parameters can be specified:
-
Name: The name for the scatter-gather iteration. The name is displayed in logs and messages and can be specified using the
setName()method. -
Parallelism: The parallelism for the iteration. It can be set using the
setParallelism()method. -
Solution set in unmanaged memory: Defines whether the solution set is kept in managed memory (Flink’s internal way of keeping objects in serialized form) or as a simple object map. By default, the solution set runs in managed memory. This property can be set using the
setSolutionSetUnmanagedMemory()method. -
Aggregators: Iteration aggregators can be registered using the
registerAggregator()method. An iteration aggregator combines all aggregates globally once per superstep and makes them available in the next superstep. Registered aggregators can be accessed inside the user-definedScatterFunctionandGatherFunction. -
Broadcast Variables: DataSets can be added as Broadcast Variables to the
ScatterFunctionandGatherFunction, using theaddBroadcastSetForUpdateFunction()andaddBroadcastSetForMessagingFunction()methods, respectively. -
Number of Vertices: Accessing the total number of vertices within the iteration. This property can be set using the
setOptNumVertices()method. The number of vertices can then be accessed in the vertex update function and in the messaging function using thegetNumberOfVertices()method. If the option is not set in the configuration, this method will return -1. -
Degrees: Accessing the in/out degree for a vertex within an iteration. This property can be set using the
setOptDegrees()method. The in/out degrees can then be accessed in the vertex update function and in the messaging function, per vertex using thegetInDegree()andgetOutDegree()methods. If the degrees option is not set in the configuration, these methods will return -1. -
Messaging Direction: By default, a vertex sends messages to its out-neighbors and updates its value based on messages received from its in-neighbors. This configuration option allows users to change the messaging direction to either
EdgeDirection.IN,EdgeDirection.OUT,EdgeDirection.ALL. The messaging direction also dictates the update direction which would beEdgeDirection.OUT,EdgeDirection.INandEdgeDirection.ALL, respectively. This property can be set using thesetDirection()method.
Graph<Long, Double, Double> graph = ...
// configure the iteration
ScatterGatherConfiguration parameters = new ScatterGatherConfiguration();
// set the iteration name
parameters.setName("Gelly Iteration");
// set the parallelism
parameters.setParallelism(16);
// register an aggregator
parameters.registerAggregator("sumAggregator", new LongSumAggregator());
// run the scatter-gather iteration, also passing the configuration parameters
Graph<Long, Double, Double> result =
graph.runScatterGatherIteration(
new Messenger(), new VertexUpdater(), maxIterations, parameters);
// user-defined functions
public static final class Messenger extends ScatterFunction {...}
public static final class VertexUpdater extends GatherFunction {
LongSumAggregator aggregator = new LongSumAggregator();
public void preSuperstep() {
// retrieve the Aggregator
aggregator = getIterationAggregator("sumAggregator");
}
public void updateVertex(Vertex<Long, Long> vertex, MessageIterator inMessages) {
//do some computation
Long partialValue = ...
// aggregate the partial value
aggregator.aggregate(partialValue);
// update the vertex value
setNewVertexValue(...);
}
}val graph: Graph[Long, Double, Double] = ...
val parameters = new ScatterGatherConfiguration
// set the iteration name
parameters.setName("Gelly Iteration")
// set the parallelism
parameters.setParallelism(16)
// register an aggregator
parameters.registerAggregator("sumAggregator", new LongSumAggregator)
// run the scatter-gather iteration, also passing the configuration parameters
val result = graph.runScatterGatherIteration(new Messenger, new VertexUpdater, maxIterations, parameters)
// user-defined functions
final class Messenger extends ScatterFunction {...}
final class VertexUpdater extends GatherFunction {
var aggregator = new LongSumAggregator
override def preSuperstep {
// retrieve the Aggregator
aggregator = getIterationAggregator("sumAggregator")
}
override def updateVertex(vertex: Vertex[Long, Long], inMessages: MessageIterator[Long]) {
//do some computation
val partialValue = ...
// aggregate the partial value
aggregator.aggregate(partialValue)
// update the vertex value
setNewVertexValue(...)
}
}The following example illustrates the usage of the degree as well as the number of vertices options.
Graph<Long, Double, Double> graph = ...
// configure the iteration
ScatterGatherConfiguration parameters = new ScatterGatherConfiguration();
// set the number of vertices option to true
parameters.setOptNumVertices(true);
// set the degree option to true
parameters.setOptDegrees(true);
// run the scatter-gather iteration, also passing the configuration parameters
Graph<Long, Double, Double> result =
graph.runScatterGatherIteration(
new Messenger(), new VertexUpdater(), maxIterations, parameters);
// user-defined functions
public static final class Messenger extends ScatterFunction {
...
// retrieve the vertex out-degree
outDegree = getOutDegree();
...
}
public static final class VertexUpdater extends GatherFunction {
...
// get the number of vertices
long numVertices = getNumberOfVertices();
...
}val graph: Graph[Long, Double, Double] = ...
// configure the iteration
val parameters = new ScatterGatherConfiguration
// set the number of vertices option to true
parameters.setOptNumVertices(true)
// set the degree option to true
parameters.setOptDegrees(true)
// run the scatter-gather iteration, also passing the configuration parameters
val result = graph.runScatterGatherIteration(new Messenger, new VertexUpdater, maxIterations, parameters)
// user-defined functions
final class Messenger extends ScatterFunction {
...
// retrieve the vertex out-degree
val outDegree = getOutDegree
...
}
final class VertexUpdater extends GatherFunction {
...
// get the number of vertices
val numVertices = getNumberOfVertices
...
}The following example illustrates the usage of the edge direction option. Vertices update their values to contain a list of all their in-neighbors.
Graph<Long, HashSet<Long>, Double> graph = ...
// configure the iteration
ScatterGatherConfiguration parameters = new ScatterGatherConfiguration();
// set the messaging direction
parameters.setDirection(EdgeDirection.IN);
// run the scatter-gather iteration, also passing the configuration parameters
DataSet<Vertex<Long, HashSet<Long>>> result =
graph.runScatterGatherIteration(
new Messenger(), new VertexUpdater(), maxIterations, parameters)
.getVertices();
// user-defined functions
public static final class Messenger extends GatherFunction {...}
public static final class VertexUpdater extends ScatterFunction {...}val graph: Graph[Long, HashSet[Long], Double] = ...
// configure the iteration
val parameters = new ScatterGatherConfiguration
// set the messaging direction
parameters.setDirection(EdgeDirection.IN)
// run the scatter-gather iteration, also passing the configuration parameters
val result = graph.runScatterGatherIteration(new Messenger, new VertexUpdater, maxIterations, parameters)
.getVertices
// user-defined functions
final class Messenger extends ScatterFunction {...}
final class VertexUpdater extends GatherFunction {...}Gather-Sum-Apply Iterations
Like in the scatter-gather model, Gather-Sum-Apply also proceeds in synchronized iterative steps, called supersteps. Each superstep consists of the following three phases:
- Gather: a user-defined function is invoked in parallel on the edges and neighbors of each vertex, producing a partial value.
- Sum: the partial values produced in the Gather phase are aggregated to a single value, using a user-defined reducer.
- Apply: each vertex value is updated by applying a function on the current value and the aggregated value produced by the Sum phase.
Let us consider computing Single-Source-Shortest-Paths with GSA on the following graph and let vertex 1 be the source. During the Gather phase, we calculate the new candidate distances, by adding each vertex value with the edge weight. In Sum, the candidate distances are grouped by vertex ID and the minimum distance is chosen. In Apply, the newly calculated distance is compared to the current vertex value and the minimum of the two is assigned as the new value of the vertex.
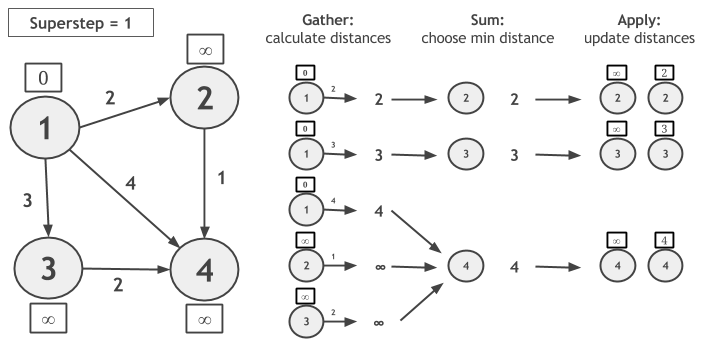
Notice that, if a vertex does not change its value during a superstep, it will not calculate candidate distance during the next superstep. The algorithm converges when no vertex changes value.
To implement this example in Gelly GSA, the user only needs to call the runGatherSumApplyIteration method on the input graph and provide the GatherFunction, SumFunction and ApplyFunction UDFs. Iteration synchronization, grouping, value updates and convergence are handled by the system:
// read the input graph
Graph<Long, Double, Double> graph = ...
// define the maximum number of iterations
int maxIterations = 10;
// Execute the GSA iteration
Graph<Long, Double, Double> result = graph.runGatherSumApplyIteration(
new CalculateDistances(), new ChooseMinDistance(), new UpdateDistance(), maxIterations);
// Extract the vertices as the result
DataSet<Vertex<Long, Double>> singleSourceShortestPaths = result.getVertices();
// - - - UDFs - - - //
// Gather
private static final class CalculateDistances extends GatherFunction<Double, Double, Double> {
public Double gather(Neighbor<Double, Double> neighbor) {
return neighbor.getNeighborValue() + neighbor.getEdgeValue();
}
}
// Sum
private static final class ChooseMinDistance extends SumFunction<Double, Double, Double> {
public Double sum(Double newValue, Double currentValue) {
return Math.min(newValue, currentValue);
}
}
// Apply
private static final class UpdateDistance extends ApplyFunction<Long, Double, Double> {
public void apply(Double newDistance, Double oldDistance) {
if (newDistance < oldDistance) {
setResult(newDistance);
}
}
}// read the input graph
val graph: Graph[Long, Double, Double] = ...
// define the maximum number of iterations
val maxIterations = 10
// Execute the GSA iteration
val result = graph.runGatherSumApplyIteration(new CalculateDistances, new ChooseMinDistance, new UpdateDistance, maxIterations)
// Extract the vertices as the result
val singleSourceShortestPaths = result.getVertices
// - - - UDFs - - - //
// Gather
final class CalculateDistances extends GatherFunction[Double, Double, Double] {
override def gather(neighbor: Neighbor[Double, Double]): Double = {
neighbor.getNeighborValue + neighbor.getEdgeValue
}
}
// Sum
final class ChooseMinDistance extends SumFunction[Double, Double, Double] {
override def sum(newValue: Double, currentValue: Double): Double = {
Math.min(newValue, currentValue)
}
}
// Apply
final class UpdateDistance extends ApplyFunction[Long, Double, Double] {
override def apply(newDistance: Double, oldDistance: Double) = {
if (newDistance < oldDistance) {
setResult(newDistance)
}
}
}Note that gather takes a Neighbor type as an argument. This is a convenience type which simply wraps a vertex with its neighboring edge.
For more examples of how to implement algorithms with the Gather-Sum-Apply model, check the GSAPageRank and GSAConnectedComponents library methods of Gelly.
Configuring a Gather-Sum-Apply Iteration
A GSA iteration can be configured using a GSAConfiguration object.
Currently, the following parameters can be specified:
-
Name: The name for the GSA iteration. The name is displayed in logs and messages and can be specified using the
setName()method. -
Parallelism: The parallelism for the iteration. It can be set using the
setParallelism()method. -
Solution set in unmanaged memory: Defines whether the solution set is kept in managed memory (Flink’s internal way of keeping objects in serialized form) or as a simple object map. By default, the solution set runs in managed memory. This property can be set using the
setSolutionSetUnmanagedMemory()method. -
Aggregators: Iteration aggregators can be registered using the
registerAggregator()method. An iteration aggregator combines all aggregates globally once per superstep and makes them available in the next superstep. Registered aggregators can be accessed inside the user-definedGatherFunction,SumFunctionandApplyFunction. -
Broadcast Variables: DataSets can be added as Broadcast Variables to the
GatherFunction,SumFunctionandApplyFunction, using the methodsaddBroadcastSetForGatherFunction(),addBroadcastSetForSumFunction()andaddBroadcastSetForApplyFunctionmethods, respectively. -
Number of Vertices: Accessing the total number of vertices within the iteration. This property can be set using the
setOptNumVertices()method. The number of vertices can then be accessed in the gather, sum and/or apply functions by using thegetNumberOfVertices()method. If the option is not set in the configuration, this method will return -1. -
Neighbor Direction: By default values are gathered from the out neighbors of the Vertex. This can be modified using the
setDirection()method.
The following example illustrates the usage of the number of vertices option.
Graph<Long, Double, Double> graph = ...
// configure the iteration
GSAConfiguration parameters = new GSAConfiguration();
// set the number of vertices option to true
parameters.setOptNumVertices(true);
// run the gather-sum-apply iteration, also passing the configuration parameters
Graph<Long, Long, Long> result = graph.runGatherSumApplyIteration(
new Gather(), new Sum(), new Apply(),
maxIterations, parameters);
// user-defined functions
public static final class Gather {
...
// get the number of vertices
long numVertices = getNumberOfVertices();
...
}
public static final class Sum {
...
// get the number of vertices
long numVertices = getNumberOfVertices();
...
}
public static final class Apply {
...
// get the number of vertices
long numVertices = getNumberOfVertices();
...
}val graph: Graph[Long, Double, Double] = ...
// configure the iteration
val parameters = new GSAConfiguration
// set the number of vertices option to true
parameters.setOptNumVertices(true)
// run the gather-sum-apply iteration, also passing the configuration parameters
val result = graph.runGatherSumApplyIteration(new Gather, new Sum, new Apply, maxIterations, parameters)
// user-defined functions
final class Gather {
...
// get the number of vertices
val numVertices = getNumberOfVertices
...
}
final class Sum {
...
// get the number of vertices
val numVertices = getNumberOfVertices
...
}
final class Apply {
...
// get the number of vertices
val numVertices = getNumberOfVertices
...
}The following example illustrates the usage of the edge direction option.
Graph<Long, HashSet<Long>, Double> graph = ...
// configure the iteration
GSAConfiguration parameters = new GSAConfiguration();
// set the messaging direction
parameters.setDirection(EdgeDirection.IN);
// run the gather-sum-apply iteration, also passing the configuration parameters
DataSet<Vertex<Long, HashSet<Long>>> result =
graph.runGatherSumApplyIteration(
new Gather(), new Sum(), new Apply(), maxIterations, parameters)
.getVertices();val graph: Graph[Long, HashSet[Long], Double] = ...
// configure the iteration
val parameters = new GSAConfiguration
// set the messaging direction
parameters.setDirection(EdgeDirection.IN)
// run the gather-sum-apply iteration, also passing the configuration parameters
val result = graph.runGatherSumApplyIteration(new Gather, new Sum, new Apply, maxIterations, parameters)
.getVertices()Iteration Abstractions Comparison
Although the three iteration abstractions in Gelly seem quite similar, understanding their differences can lead to more performant and maintainable programs. Among the three, the vertex-centric model is the most general model and supports arbitrary computation and messaging for each vertex. In the scatter-gather model, the logic of producing messages is decoupled from the logic of updating vertex values. Thus, programs written using scatter-gather are sometimes easier to follow and maintain. Separating the messaging phase from the vertex value update logic not only makes some programs easier to follow but might also have a positive impact on performance. Scatter-gather implementations typically have lower memory requirements, because concurrent access to the inbox (messages received) and outbox (messages to send) data structures is not required. However, this characteristic also limits expressiveness and makes some computation patterns non-intuitive. Naturally, if an algorithm requires a vertex to concurrently access its inbox and outbox, then the expression of this algorithm in scatter-gather might be problematic. Strongly Connected Components and Approximate Maximum Weight Matching are examples of such graph algorithms. A direct consequence of this restriction is that vertices cannot generate messages and update their states in the same phase. Thus, deciding whether to propagate a message based on its content would require storing it in the vertex value, so that the gather phase has access to it, in the following iteration step. Similarly, if the vertex update logic includes computation over the values of the neighboring edges, these have to be included inside a special message passed from the scatter to the gather phase. Such workarounds often lead to higher memory requirements and non-elegant, hard to understand algorithm implementations.
Gather-sum-apply iterations are also quite similar to scatter-gather iterations. In fact, any algorithm which can be expressed as a GSA iteration can also be written in the scatter-gather model. The messaging phase of the scatter-gather model is equivalent to the Gather and Sum steps of GSA: Gather can be seen as the phase where the messages are produced and Sum as the phase where they are routed to the target vertex. Similarly, the value update phase corresponds to the Apply step.
The main difference between the two implementations is that the Gather phase of GSA parallelizes the computation over the edges, while the messaging phase distributes the computation over the vertices. Using the SSSP examples above, we see that in the first superstep of the scatter-gather case, vertices 1, 2 and 3 produce messages in parallel. Vertex 1 produces 3 messages, while vertices 2 and 3 produce one message each. In the GSA case on the other hand, the computation is parallelized over the edges: the three candidate distance values of vertex 1 are produced in parallel. Thus, if the Gather step contains “heavy” computation, it might be a better idea to use GSA and spread out the computation, instead of burdening a single vertex. Another case when parallelizing over the edges might prove to be more efficient is when the input graph is skewed (some vertices have a lot more neighbors than others).
Another difference between the two implementations is that the scatter-gather implementation uses a coGroup operator internally, while GSA uses a reduce. Therefore, if the function that combines neighbor values (messages) requires the whole group of values for the computation, scatter-gather should be used. If the update function is associative and commutative, then the GSA’s reducer is expected to give a more efficient implementation, as it can make use of a combiner.
Another thing to note is that GSA works strictly on neighborhoods, while in the vertex-centric and scatter-gather models, a vertex can send a message to any vertex, given that it knows its vertex ID, regardless of whether it is a neighbor. Finally, in Gelly’s scatter-gather implementation, one can choose the messaging direction, i.e. the direction in which updates propagate. GSA does not support this yet, so each vertex will be updated based on the values of its in-neighbors only.
The main differences among the Gelly iteration models are shown in the table below.
| Iteration Model | Update Function | Update Logic | Communication Scope | Communication Logic |
|---|---|---|---|---|
| Vertex-Centric | arbitrary | arbitrary | any vertex | arbitrary |
| Scatter-Gather | arbitrary | based on received messages | any vertex | based on vertex state |
| Gather-Sum-Apply | associative and commutative | based on neighbors' values | neighborhood | based on vertex state |
Graph Validation
Gelly provides a simple utility for performing validation checks on input graphs. Depending on the application context, a graph may or may not be valid according to certain criteria. For example, a user might need to validate whether their graph contains duplicate edges or whether its structure is bipartite. In order to validate a graph, one can define a custom GraphValidator and implement its validate() method. InvalidVertexIdsValidator is Gelly’s pre-defined validator. It checks that the edge set contains valid vertex IDs, i.e. that all edge IDs
also exist in the vertex IDs set.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
// create a list of vertices with IDs = {1, 2, 3, 4, 5}
List<Vertex<Long, Long>> vertices = ...
// create a list of edges with IDs = {(1, 2) (1, 3), (2, 4), (5, 6)}
List<Edge<Long, Long>> edges = ...
Graph<Long, Long, Long> graph = Graph.fromCollection(vertices, edges, env);
// will return false: 6 is an invalid ID
graph.validate(new InvalidVertexIdsValidator<Long, Long, Long>());val env = ExecutionEnvironment.getExecutionEnvironment
// create a list of vertices with IDs = {1, 2, 3, 4, 5}
val vertices: List[Vertex[Long, Long]] = ...
// create a list of edges with IDs = {(1, 2) (1, 3), (2, 4), (5, 6)}
val edges: List[Edge[Long, Long]] = ...
val graph = Graph.fromCollection(vertices, edges, env)
// will return false: 6 is an invalid ID
graph.validate(new InvalidVertexIdsValidator[Long, Long, Long])Library Methods
Gelly has a growing collection of graph algorithms for easily analyzing large-scale Graphs. So far, the following library methods are implemented:
- Community Detection
- Label Propagation
- Connected Components
- GSA Connected Components
- PageRank
- GSA PageRank
- Single Source Shortest Paths
- GSA Single Source Shortest Paths
- Triangle Count
- Triangle Enumerator
- Hyperlink-Induced Topic Search
- Summarization
- Adamic-Adar
- Jaccard Index
- Local Clustering Coefficient
- Global Clustering Coefficient
Gelly’s library methods can be used by simply calling the run() method on the input graph:
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
Graph<Long, Long, NullValue> graph = ...
// run Label Propagation for 30 iterations to detect communities on the input graph
DataSet<Vertex<Long, Long>> verticesWithCommunity = graph.run(new LabelPropagation<Long>(30));
// print the result
verticesWithCommunity.print();val env = ExecutionEnvironment.getExecutionEnvironment
val graph: Graph[java.lang.Long, java.lang.Long, NullValue] = ...
// run Label Propagation for 30 iterations to detect communities on the input graph
val verticesWithCommunity = graph.run(new LabelPropagation[java.lang.Long, java.lang.Long, NullValue](30))
// print the result
verticesWithCommunity.printCommunity Detection
Overview
In graph theory, communities refer to groups of nodes that are well connected internally, but sparsely connected to other groups. This library method is an implementation of the community detection algorithm described in the paper Towards real-time community detection in large networks.
Details
The algorithm is implemented using scatter-gather iterations.
Initially, each vertex is assigned a Tuple2 containing its initial value along with a score equal to 1.0.
In each iteration, vertices send their labels and scores to their neighbors. Upon receiving messages from its neighbors,
a vertex chooses the label with the highest score and subsequently re-scores it using the edge values,
a user-defined hop attenuation parameter, delta, and the superstep number.
The algorithm converges when vertices no longer update their value or when the maximum number of iterations
is reached.
Usage
The algorithm takes as input a Graph with any vertex type, Long vertex values, and Double edge values. It returns a Graph of the same type as the input,
where the vertex values correspond to the community labels, i.e. two vertices belong to the same community if they have the same vertex value.
The constructor takes two parameters:
maxIterations: the maximum number of iterations to run.delta: the hop attenuation parameter, with default value 0.5.
Label Propagation
Overview
This is an implementation of the well-known Label Propagation algorithm described in this paper. The algorithm discovers communities in a graph, by iteratively propagating labels between neighbors. Unlike the Community Detection library method, this implementation does not use scores associated with the labels.
Details
The algorithm is implemented using scatter-gather iterations.
Labels are expected to be of type Comparable and are initialized using the vertex values of the input Graph.
The algorithm iteratively refines discovered communities by propagating labels. In each iteration, a vertex adopts
the label that is most frequent among its neighbors’ labels. In case of a tie (i.e. two or more labels appear with the
same frequency), the algorithm picks the greater label. The algorithm converges when no vertex changes its value or
the maximum number of iterations has been reached. Note that different initializations might lead to different results.
Usage
The algorithm takes as input a Graph with a Comparable vertex type, a Comparable vertex value type and an arbitrary edge value type.
It returns a DataSet of vertices, where the vertex value corresponds to the community in which this vertex belongs after convergence.
The constructor takes one parameter:
maxIterations: the maximum number of iterations to run.
Connected Components
Overview
This is an implementation of the Weakly Connected Components algorithm. Upon convergence, two vertices belong to the same component, if there is a path from one to the other, without taking edge direction into account.
Details
The algorithm is implemented using scatter-gather iterations. This implementation uses a comparable vertex value as initial component identifier (ID). Vertices propagate their current value in each iteration. Upon receiving component IDs from its neighbors, a vertex adopts a new component ID if its value is lower than its current component ID. The algorithm converges when vertices no longer update their component ID value or when the maximum number of iterations has been reached.
Usage
The result is a DataSet of vertices, where the vertex value corresponds to the assigned component.
The constructor takes one parameter:
maxIterations: the maximum number of iterations to run.
GSA Connected Components
Overview
This is an implementation of the Weakly Connected Components algorithm. Upon convergence, two vertices belong to the same component, if there is a path from one to the other, without taking edge direction into account.
Details
The algorithm is implemented using gather-sum-apply iterations. This implementation uses a comparable vertex value as initial component identifier (ID). In the gather phase, each vertex collects the vertex value of their adjacent vertices. In the sum phase, the minimum among those values is selected. In the apply phase, the algorithm sets the minimum value as the new vertex value if it is smaller than the current value. The algorithm converges when vertices no longer update their component ID value or when the maximum number of iterations has been reached.
Usage
The result is a DataSet of vertices, where the vertex value corresponds to the assigned component.
The constructor takes one parameter:
maxIterations: the maximum number of iterations to run.
PageRank
Overview
An implementation of a simple PageRank algorithm, using scatter-gather iterations. PageRank is an algorithm that was first used to rank web search engine results. Today, the algorithm and many variations, are used in various graph application domains. The idea of PageRank is that important or relevant pages tend to link to other important pages.
Details
The algorithm operates in iterations, where pages distribute their scores to their neighbors (pages they have links to) and subsequently update their scores based on the partial values they receive. The implementation assumes that each page has at least one incoming and one outgoing link. In order to consider the importance of a link from one page to another, scores are divided by the total number of out-links of the source page. Thus, a page with 10 links will distribute 1/10 of its score to each neighbor, while a page with 100 links, will distribute 1/100 of its score to each neighboring page. This process computes what is often called the transition probablities, i.e. the probability that some page will lead to other page while surfing the web. To correctly compute the transition probabilities, this implementation expects the edge values to be initialised to 1.0.
Usage
The algorithm takes as input a Graph with any vertex type, Double vertex values, and Double edge values. Edges values should be initialized to 1.0, in order to correctly compute the transition probabilities. Otherwise, the transition probability for an Edge (u, v) will be set to the edge value divided by u’s out-degree. The algorithm returns a DataSet of vertices, where the vertex value corresponds to assigned rank after convergence (or maximum iterations).
The constructors take the following parameters:
beta: the damping factor.maxIterations: the maximum number of iterations to run.
GSA PageRank
The algorithm is implemented using gather-sum-apply iterations.
See the PageRank library method for implementation details and usage information.
Single Source Shortest Paths
Overview
An implementation of the Single-Source-Shortest-Paths algorithm for weighted graphs. Given a source vertex, the algorithm computes the shortest paths from this source to all other nodes in the graph.
Details
The algorithm is implemented using scatter-gather iterations. In each iteration, a vertex sends to its neighbors a message containing the sum its current distance and the edge weight connecting this vertex with the neighbor. Upon receiving candidate distance messages, a vertex calculates the minimum distance and, if a shorter path has been discovered, it updates its value. If a vertex does not change its value during a superstep, then it does not produce messages for its neighbors for the next superstep. The computation terminates after the specified maximum number of supersteps or when there are no value updates.
Usage
The algorithm takes as input a Graph with any vertex type, Double vertex values, and Double edge values. The output is a DataSet of vertices where the vertex values
correspond to the minimum distances from the given source vertex.
The constructor takes two parameters:
srcVertexIdThe vertex ID of the source vertex.maxIterations: the maximum number of iterations to run.
GSA Single Source Shortest Paths
The algorithm is implemented using gather-sum-apply iterations.
See the Single Source Shortest Paths library method for implementation details and usage information.
Triangle Count
Overview
An analytic for counting the number of unique triangles in a graph.
Details
Counts the triangles generated by Triangle Listing.
Usage
The analytic takes an undirected graph as input and returns as a result a Long corresponding to the number of triangles
in the graph. The graph ID type must be Comparable and Copyable.
Triangle Listing
This algorithm supports object reuse. The graph ID type must be Comparable and Copyable.
See the Triangle Enumerator library method for implementation details.
Triangle Enumerator
Overview
This library method enumerates unique triangles present in the input graph. A triangle consists of three edges that connect three vertices with each other. This implementation ignores edge directions.
Details
The basic triangle enumeration algorithm groups all edges that share a common vertex and builds triads, i.e., triples of vertices that are connected by two edges. Then, all triads are filtered for which no third edge exists that closes the triangle. For a group of n edges that share a common vertex, the number of built triads is quadratic ((n*(n-1))/2). Therefore, an optimization of the algorithm is to group edges on the vertex with the smaller output degree to reduce the number of triads. This implementation extends the basic algorithm by computing output degrees of edge vertices and grouping on edges on the vertex with the smaller degree.
Usage
The algorithm takes a directed graph as input and outputs a DataSet of Tuple3. The Vertex ID type has to be Comparable.
Each Tuple3 corresponds to a triangle, with the fields containing the IDs of the vertices forming the triangle.
Hyperlink-Induced Topic Search
Overview
Hyperlink-Induced Topic Search (HITS, or “Hubs and Authorities”) computes two interdependent scores for every vertex in a directed graph. Good hubs are those which point to many good authorities and good authorities are those pointed to by many good hubs.
Details
Every vertex is assigned the same initial hub and authority scores. The algorithm then iteratively updates the scores until termination. During each iteration new hub scores are computed from the authority scores, then new authority scores are computed from the new hub scores. The scores are then normalized and optionally tested for convergence.
Usage
The algorithm takes a directed graph as input and outputs a DataSet of Tuple3 containing the vertex ID, hub score,
and authority score.
Summarization
Overview
The summarization algorithm computes a condensed version of the input graph by grouping vertices and edges based on their values. In doing so, the algorithm helps to uncover insights about patterns and distributions in the graph. One possible use case is the visualization of communities where the whole graph is too large and needs to be summarized based on the community identifier stored at a vertex.
Details
In the resulting graph, each vertex represents a group of vertices that share the same value. An edge, that connects a vertex with itself, represents all edges with the same edge value that connect vertices from the same vertex group. An edge between different vertices in the output graph represents all edges with the same edge value between members of different vertex groups in the input graph.
The algorithm is implemented using Flink data operators. First, vertices are grouped by their value and a representative is chosen from each group. For any edge, the source and target vertex identifiers are replaced with the corresponding representative and grouped by source, target and edge value. Output vertices and edges are created from their corresponding groupings.
Usage
The algorithm takes a directed, vertex (and possibly edge) attributed graph as input and outputs a new graph where each vertex represents a group of vertices and each edge represents a group of edges from the input graph. Furthermore, each vertex and edge in the output graph stores the common group value and the number of represented elements.
Adamic-Adar
Overview
Adamic-Adar measures the similarity between pairs of vertices as the sum of the inverse logarithm of degree over shared neighbors. Scores are non-negative and unbounded. A vertex with higher degree has greater overall influence but is less influential to each pair of neighbors.
Details
The algorithm first annotates each vertex with the inverse of the logarithm of the vertex degree then joins this score onto edges by source vertex. Grouping on the source vertex, each pair of neighbors is emitted with the vertex score. Grouping on two-paths, the Adamic-Adar score is summed.
See the Jaccard Index library method for a similar algorithm.
Usage
The algorithm takes a simple, undirected graph as input and outputs a DataSet of tuples containing two vertex IDs and
the Adamic-Adair similarity score. The graph ID type must be Comparable and Copyable.
setLittleParallelism: override the parallelism of operators processing small amounts of datasetMinimumRatio: filter out Adamic-Adar scores less than the given ratio times the average scoresetMinimumScore: filter out Adamic-Adar scores less than the given minimum
Jaccard Index
Overview
The Jaccard Index measures the similarity between vertex neighborhoods and is computed as the number of shared neighbors divided by the number of distinct neighbors. Scores range from 0.0 (no shared neighbors) to 1.0 (all neighbors are shared).
Details
Counting shared neighbors for pairs of vertices is equivalent to counting connecting paths of length two. The number of distinct neighbors is computed by storing the sum of degrees of the vertex pair and subtracting the count of shared neighbors, which are double-counted in the sum of degrees.
The algorithm first annotates each edge with the target vertex’s degree. Grouping on the source vertex, each pair of neighbors is emitted with the degree sum. Grouping on two-paths, the shared neighbors are counted.
Usage
The algorithm takes a simple, undirected graph as input and outputs a DataSet of tuples containing two vertex IDs,
the number of shared neighbors, and the number of distinct neighbors. The result class provides a method to compute the
Jaccard Index score. The graph ID type must be Comparable and Copyable.
setLittleParallelism: override the parallelism of operators processing small amounts of datasetMaximumScore: filter out Jaccard Index scores greater than or equal to the given maximum fractionsetMinimumScore: filter out Jaccard Index scores less than the given minimum fraction
Local Clustering Coefficient
Overview
The local clustering coefficient measures the connectedness of each vertex’s neighborhood. Scores range from 0.0 (no edges between neighbors) to 1.0 (neighborhood is a clique).
Details
An edge between a vertex’s neighbors is a triangle. Counting edges between neighbors is equivalent to counting the number of triangles which include the vertex. The clustering coefficient score is the number of edges between neighbors divided by the number of potential edges between neighbors.
See the Triangle Enumeration library method for a detailed explanation of triangle enumeration.
Usage
Directed and undirected variants are provided. The algorithms take a simple graph as input and output a DataSet of
tuples containing the vertex ID, vertex degree, and number of triangles containing the vertex. The graph ID type must be
Comparable and Copyable.
Global Clustering Coefficient
Overview
The global clustering coefficient measures the connectedness of a graph. Scores range from 0.0 (no edges between neighbors) to 1.0 (complete graph).
Details
See the Local Clustering Coefficient library method for a detailed explanation of clustering coefficient.
Usage
Directed and undirected variants are provided. The algorithm takes a simple graph as input and outputs a result
containing the total number of triplets and triangles in the graph. The graph ID type must be Comparable and
Copyable.
Graph Algorithms
The logic blocks with which the Graph API and top-level algorithms are assembled are accessible in Gelly as graph
algorithms in the org.apache.flink.graph.asm package. These algorithms provide optimization and tuning through
configuration parameters and may provide implicit runtime reuse when processing the same input with a similar
configuration.
| Algorithm | Description |
|---|---|
| degree.annotate.directed. VertexInDegree |
Annotate vertices of a directed graph with the in-degree. Optional configuration:
|
| degree.annotate.directed. VertexOutDegree |
Annotate vertices of a directed graph with the out-degree. Optional configuration:
|
| degree.annotate.directed. VertexDegrees |
Annotate vertices of a directed graph with the degree, out-degree, and in-degree. Optional configuration:
|
| degree.annotate.directed. EdgeSourceDegrees |
Annotate edges of a directed graph with the degree, out-degree, and in-degree of the source ID. Optional configuration:
|
| degree.annotate.directed. EdgeTargetDegrees |
Annotate edges of a directed graph with the degree, out-degree, and in-degree of the target ID. Optional configuration:
|
| degree.annotate.directed. EdgeDegreesPair |
Annotate edges of a directed graph with the degree, out-degree, and in-degree of both the source and target vertices. Optional configuration:
|
| degree.annotate.undirected. VertexDegree |
Annotate vertices of an undirected graph with the degree. Optional configuration:
|
| degree.annotate.undirected. EdgeSourceDegree |
Annotate edges of an undirected graph with degree of the source ID. Optional configuration:
|
| degree.annotate.undirected. EdgeTargetDegree |
Annotate edges of an undirected graph with degree of the target ID. Optional configuration:
|
| degree.annotate.undirected. EdgeDegreePair |
Annotate edges of an undirected graph with the degree of both the source and target vertices. Optional configuration:
|
| degree.filter.undirected. MaximumDegree |
Filter an undirected graph by maximum degree. Optional configuration:
|
| simple.directed. Simplify |
Remove self-loops and duplicate edges from a directed graph. Optional configuration:
|
| simple.undirected. Simplify |
Add symmetric edges and remove self-loops and duplicate edges from an undirected graph. Optional configuration:
|
| translate. TranslateGraphIds |
Translate vertex and edge IDs using the given Required configuration:
Optional configuration:
|
| translate. TranslateVertexValues |
Translate vertex values using the given Required configuration:
Optional configuration:
|
| translate. TranslateEdgeValues |
Translate edge values using the given Required configuration:
Optional configuration:
|
Graph Generators
Gelly provides a collection of scalable graph generators. Each generator is
- parallelizable, in order to create large datasets
- scale-free, generating the same graph regardless of parallelism
- thrifty, using as few operators as possible
Graph generators are configured using the builder pattern. The parallelism of generator
operators can be set explicitly by calling setParallelism(parallelism). Lowering the
parallelism will reduce the allocation of memory and network buffers.
Graph-specific configuration must be called first, then configuration common to all
generators, and lastly the call to generate(). The following example configures a
grid graph with two dimensions, configures the parallelism, and generates the graph.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
boolean wrapEndpoints = false;
int parallelism = 4;
Graph<LongValue,NullValue,NullValue> graph = new GridGraph(env)
.addDimension(2, wrapEndpoints)
.addDimension(4, wrapEndpoints)
.setParallelism(parallelism)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.GridGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
wrapEndpoints = false
val parallelism = 4
val graph = new GridGraph(env.getJavaEnv).addDimension(2, wrapEndpoints).addDimension(4, wrapEndpoints).setParallelism(parallelism).generate()Provided graph generators
- Complete Graph
- Cycle Graph
- Empty Graph
- Grid Graph
- Hypercube Graph
- Path Graph
- RMat Graph
- Singleton Edge Graph
- Star Graph
Complete Graph
An undirected graph connecting every distinct pair of vertices.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
long vertexCount = 5;
Graph<LongValue,NullValue,NullValue> graph = new CompleteGraph(env, vertexCount)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.CompleteGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
val vertexCount = 5
val graph = new CompleteGraph(env.getJavaEnv, vertexCount).generate()Cycle Graph
An undirected graph where all edges form a single cycle.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
long vertexCount = 5;
Graph<LongValue,NullValue,NullValue> graph = new CycleGraph(env, vertexCount)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.CycleGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
val vertexCount = 5
val graph = new CycleGraph(env.getJavaEnv, vertexCount).generate()Empty Graph
The graph containing no edges.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
long vertexCount = 5;
Graph<LongValue,NullValue,NullValue> graph = new EmptyGraph(env, vertexCount)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.EmptyGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
val vertexCount = 5
val graph = new EmptyGraph(env.getJavaEnv, vertexCount).generate()Grid Graph
An undirected graph connecting vertices in a regular tiling in one or more dimensions.
Each dimension is configured separately. When the dimension size is at least three the
endpoints are optionally connected by setting wrapEndpoints. Changing the following
example to addDimension(4, true) would connect 0 to 3 and 4 to 7.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
boolean wrapEndpoints = false;
Graph<LongValue,NullValue,NullValue> graph = new GridGraph(env)
.addDimension(2, wrapEndpoints)
.addDimension(4, wrapEndpoints)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.GridGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
val wrapEndpoints = false
val graph = new GridGraph(env.getJavaEnv).addDimension(2, wrapEndpoints).addDimension(4, wrapEndpoints).generate()Hypercube Graph
An undirected graph where edges form an n-dimensional hypercube. Each vertex in a hypercube connects to one other vertex in each dimension.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
long dimensions = 3;
Graph<LongValue,NullValue,NullValue> graph = new HypercubeGraph(env, dimensions)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.HypercubeGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
val dimensions = 3
val graph = new HypercubeGraph(env.getJavaEnv, dimensions).generate()Path Graph
An undirected Graph where all edges form a single path.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
long vertexCount = 5
Graph<LongValue,NullValue,NullValue> graph = new PathGraph(env, vertexCount)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.PathGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
val vertexCount = 5
val graph = new PathGraph(env.getJavaEnv, vertexCount).generate()RMat Graph
A directed or undirected power-law graph generated using the Recursive Matrix (R-Mat) model.
RMat is a stochastic generator configured with a source of randomness implementing the
RandomGenerableFactory interface. Provided implementations are JDKRandomGeneratorFactory
and MersenneTwisterFactory. These generate an initial sequence of random values which are
then used as seeds for generating the edges.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
RandomGenerableFactory<JDKRandomGenerator> rnd = new JDKRandomGeneratorFactory();
int vertexCount = 1 << scale;
int edgeCount = edgeFactor * vertexCount;
Graph<LongValue,NullValue,NullValue> graph = new RMatGraph<>(env, rnd, vertexCount, edgeCount)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.RMatGraph
val env = ExecutionEnvironment.getExecutionEnvironment
val vertexCount = 1 << scale
val edgeCount = edgeFactor * vertexCount
val graph = new RMatGraph(env.getJavaEnv, rnd, vertexCount, edgeCount).generate()The default RMat contants can be overridden as shown in the following example. The contants define the interdependence of bits from each generated edge’s source and target labels. The RMat noise can be enabled and progressively perturbs the contants while generating each edge.
The RMat generator can be configured to produce a simple graph by removing self-loops and duplicate edges. Symmetrization is performed either by a “clip-and-flip” throwing away the half matrix above the diagonal or a full “flip” preserving and mirroring all edges.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
RandomGenerableFactory<JDKRandomGenerator> rnd = new JDKRandomGeneratorFactory();
int vertexCount = 1 << scale;
int edgeCount = edgeFactor * vertexCount;
boolean clipAndFlip = false;
Graph<LongValue,NullValue,NullValue> graph = new RMatGraph<>(env, rnd, vertexCount, edgeCount)
.setConstants(0.57f, 0.19f, 0.19f)
.setNoise(true, 0.10f)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.RMatGraph
val env = ExecutionEnvironment.getExecutionEnvironment
val vertexCount = 1 << scale
val edgeCount = edgeFactor * vertexCount
clipAndFlip = false
val graph = new RMatGraph(env.getJavaEnv, rnd, vertexCount, edgeCount).setConstants(0.57f, 0.19f, 0.19f).setNoise(true, 0.10f).generate()Singleton Edge Graph
An undirected graph containing isolated two-paths.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
long vertexPairCount = 4
// note: configured with the number of vertex pairs
Graph<LongValue,NullValue,NullValue> graph = new SingletonEdgeGraph(env, vertexPairCount)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.SingletonEdgeGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
val vertexPairCount = 4
// note: configured with the number of vertex pairs
val graph = new SingletonEdgeGraph(env.getJavaEnv, vertexPairCount).generate()Star Graph
An undirected graph containing a single central vertex connected to all other leaf vertices.
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
long vertexCount = 6;
Graph<LongValue,NullValue,NullValue> graph = new StarGraph(env, vertexCount)
.generate();import org.apache.flink.api.scala._
import org.apache.flink.graph.generator.StarGraph
val env: ExecutionEnvironment = ExecutionEnvironment.getExecutionEnvironment
val vertexCount = 6
val graph = new StarGraph(env.getJavaEnv, vertexCount).generate()